アクティブ・ラーニング授業実践事例
学校名:廿日市市立大野中学校
教科等:2年数学科(平成29年1月)
単元名:三角形・四角形
数学的な表現を正しく用いて、根拠を示して説明する力を伸ばしたい
 興味や関心を高める
興味や関心を高める 互いの考えを比較する
互いの考えを比較する 知識や技能を概念化する
知識や技能を概念化する
実践の背景
- 各学年3学級の中学校で、小中一貫教育推進校です。
- 学校として育成を目指す資質・能力を「説明力」「自己有用感」と設定し、互いの考えや意見などを交流し、広げ深めていく授業づくりに、全教科で取り組んでいます。
授業改善のアプローチ
- 四角形や五角形を三角形に等積変形ができる理由を明らかにする際に、生徒自らが既習の「平行線と面積の定理」と関連付けて考えることで、深い学びにつながるように単元を構想しました。
- ペアやグループで説明を伝え合い、互いの説明を改善する学習活動を繰り返し取り入れることで、数学的に表現する力の育成につなげます。
- 前時に証明した「平行線と面積の定理」を、問題を解決するための視点として、全体で共有します。
単元づくりのポイント
目標
-
様々な事象を、平行線の性質、三角形の合同条件、三角形や四角形の性質などで捉えたり、平面図形の基本的な性質や関係を見いだしたりするなど、数学的に考え表現することに関心をもち、意欲的に数学の問題に活用して考えたり判断したりしようとする。
【数学への関心・意欲・態度】 -
平行線の性質、三角形の合同条件、三角形や四角形の性質などについての基礎的・基本的な知識及び技能を活用しながら、事象を数学的な推論の方法を用いて論理的に表現したり、その過程を振り返って考えを深めたりするなど、数学的な見方や考え方を身に付ける。
【数学的な見方や考え方】 - 二等辺三角形や平行四辺形の性質などを記号を用いて表したり、その意味を読み取ったりするなど、技能を身に付ける。
【数学的な技能】 - 二等辺三角形の性質、平行四辺形の性質や平行四辺形になるための条件、直角三角形の合同条件、四角形の包摂関係などを理解し、知識を身に付ける。
【数量・図形などについての知識・理解】
展開
三角形・四角形(全19時間扱い中第17時)
- 1 基本的な図形の性質(1)
-
- 折り紙を使って、視覚的に図形を捉え、三角形や四角形の性質を調べる。
- 2 二等辺三角形(4)
-
- 二等辺三角形と正三角形の性質を証明する。
- 命題の逆を示し、証明する。
- 3 直角三角形の合同(2)
-
- 直角三角形の合同条件を用いて、図形の性質を証明する。
- 4 平行四辺形の性質(3)
-
- 平行四辺形の性質などを証明する。
- 5 平行四辺形になるための条件(3)
-
- 平行四辺形になるための条件を証明する。
- 平行四辺形になるための条件を用いて、図形の性質を証明する。
- 6 特別な平行四辺形(2)
-
- 平行四辺形と長方形、ひし形、正方形の包摂関係を説明する。
- 平行四辺形が、長方形、ひし形、正方形になるための条件を調べる。
- 7 平行線と面積(2)本時
-
- 平行線と面積の定理を用いて、多角形を等積変形し、その理由を説明する。
- 8 単元のまとめ(2)
-
- 折り紙を折ってできた図形が持っている性質を証明する。
「主体的・対話的で深い学び」の視点からの授業改善
本時のねらい
- 平行線と面積の定理を使って、四角形や五角形を三角形に等積変形する方法とその方法が正しい理由が説明できる。
授業場面より
-
①四角形を三角形に等積変形するための視点を共有する
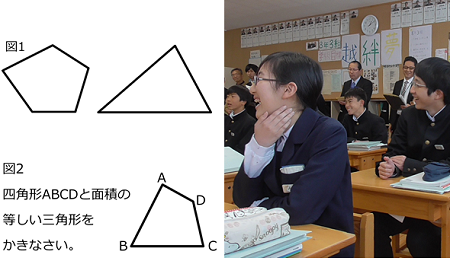
「五角形と三角形の面積はどちらが大きいと思いますか」と、教師は辺の長さを示していない図を生徒に示します。(図1)
「五角形が小さく見えるね」、「辺の長さが知りたいな」と生徒はつぶやきます。教師は、「2つの図形の面積が等しい」ことを伝え、「四角形ABCDと面積が等しい三角形をかき、数学的な表現を使って理由も説明しよう(図2)」と問題を示します。
前時に学習した「平行線と面積の定理」を振り返る生徒、四角形の対角線をかいて2つの三角形に分けて考える生徒、面積が等しいことを確かめるために必要な条件を考える中で、「平行線」と「底辺を共有する高さが等しい三角形」に着目すれば問題の解決につながることに気付いている生徒の姿と捉えられます。 -
②四角形が三角形に等積変形できる理由を考える

生徒は「どの三角形に着目し、四角形ABCDのどこに平行線をひけばよいか」、「平行線と面積の定理」の考えが適用できるように、個で考えたことをグループで伝え合っていきます。
あるグループでは、「△ACDのどこを底辺として考えればよいか」という疑問についてメンバーで意見を交わします。「△ACDと底辺が共通で高さが等しい三角形を見つければ等積変形ができそうだから、対角線ACを底辺とすればよい」という視点を共有し、個で問題を解決するための方法と理由を考えていきます。
教師は、困難さを感じているグループに対し、「点Dをどこに動かすか、およその位置を予想して図に示す」ように働き掛けます。生徒は、点Dの移動先のおよその位置を図に示すことで、「ACを底辺とし、ACに平行で点Dを通る直線を引けば、△ACDと面積が等しい三角形がかけそうだ」という解決に向けた方法を明らかにすることにつながりました。 -
③考えた方法が正しい理由をペアで伝え合う

全体で四角形ABCDと面積が等しい三角形をかく方法を確かめたあと、教師は、それぞれの生徒が考えた方法が正しい理由をペアで伝え合うように働き掛けます。すべての生徒が数学的な表現を用い、相手に納得してもらえる説明ができるようにするためです。
生徒は説明を伝える際に相手がワークシートを読みやすい向きにするとともに、図の三角形の底辺と高さ、平行線を指で示しながら、根拠を明らかにして理由を説明していきます。
数学的な表現を使って、根拠を明らかにして説明できているところを生徒同士が認め合い、根拠が明らかではない点を指摘し合うことで、自らの説明を修正し、よりよいものに改める姿も見られました。 -
④本時の学びを振り返る

本時のまとめとして、「五角形を三角形に等積変形し、その方法が正しいことを説明する」という条件をかえた発展的な問題を教師は提示します。生徒は学習を振り返りながら、五角形の対角線をひいてできる三角形に着目して問題を解決していきました。
「四角形を三角形に等積変形したときと同じように五角形でも…」と、生徒が理由を説明する姿から、既習事項と結びつけて考えていると捉えられます。
生徒が仲間とともに対話を通して問題を解決する過程で、既習の「平行線と面積の定理」を適用して考え、等積変形の方法が正しいといえる理由を、数学的な表現を用いて説明する力の育成にもつながっているといえます。
報告者:研修協力員 木野村

