アクティブ・ラーニング授業実践事例
学校名:由利本荘市立西目中学校
教科等:2年数学科(平成28年11月)
単元名:平行と合同
事象を数量や図形及びそれらの関係などに着目して捉え、論理的に考える力を育成したい
 振り返って次へつなげる
振り返って次へつなげる 互いの考えを比較する
互いの考えを比較する 知識・技能を活用する
知識・技能を活用する
実践の背景
- 実践校は「立志の学校」です。高い志を持ち、将来に渡って力強く生き抜く人間を育てることを理念としています。また、コミュニティ・スクールとして、地域とともに学校づくりを進めています。
- 開発実践フィールド校として、全職員でアクティブ・ラーニングの視点からの授業改善に取り組む過程を、県教育委員会・市教育委員会・県総合教育センターと連携し、推進地域に公開をしながら進めています。
- 学校で育てたい資質・能力を全職員で話し合い、それに向けて各教科で具体的な取組を積み重ね、取組を日常化シートに教師の手立てと子供の変容について記入し、共有、検証しながら研究を進めています。
授業改善のアプローチ
本単元では、三角形や四角形などの多角形の角の大きさについての性質を、論理的に筋道を立てた数学的な推論を行って調べることができるようにしていきます。その際、図形をよく観察したり、作図したりする操作や実験などの活動を通して、その推論の過程を自分の言葉で他者に分かりやすく表現することを大切にしていきます。また、図形の合同について理解し図形についての見方を深めるとともに、図形の性質を三角形の合同条件などを基にして演繹的に確かめ、論理的に考察し表現することも大切にしていきます。
数学的な推論には、主なものとして帰納、類推、演繹があり、それらは数や図形の性質などを見いだしたり、数学を利用したり、数学的に説明し伝え合ったりする際に重要なはたらきをします。帰納は、特別な場合についての観察、操作や実験などの活動に基づいて、それらを含んだより一般的な結果を導き出す推論です。また、類推は、似たような条件のもとでは、似たような結果が成り立つであろうと考えて、新しい命題を予想する推論です。帰納や類推は、数や図形の性質などを見いだすための大切な推論ですが、導かれた事柄は、必ずしも正しいとは限りません。帰納や類推によって導かれた事柄がいつでも正しいかどうかは、演繹により確かめられます。本単元で扱う演繹は、前提となる命題から論理の規則に従って必然的な結論を導き出す推論です。
例えば、いくつかの三角形の内角の大きさを実測するなどの帰納により、「三角形の内角の和は180°である」ことを導いた場合、「すべての三角形の内角の和は180°である」ことが正しいかどうかは分かりません。本単元では、このことを求めるために、平行線の性質などを根拠とした演繹によることの必要性を大切にしていきます。また、対頂角の性質を考える場合、測定に基づいて確認するだけではなく、根拠を明らかにし、それを基にして筋道を立てて説明する活動を行うことによって、証明の学習につなげていきます。帰納や類推により予想したことを演繹によって確かめることは、内容の理解を深めるとともに、知識を関連付け、さらに体系化するのにも役立つと考えています。
本時では、単元の終末として角度を求めるために三角形の合同を用いて考える問題を準備し、これまでの学習を総合的に捉えられるようにしていきます。学習過程では生徒が問題から様々な情報を見いだし、さらにはその情報を結びつけて考えていくことを大切にしていきます。単元を通して、事象を数量や図形及びそれらの関係などに着目して捉えることで、論理的に考える力を育成したいと考え、授業を構築しました。
単元づくりのポイント
目標
- 様々な事象を、平行線の性質や三角形の角、三角形の合同条件で捉えたりするなど、数学的に考え表現することに関心をもち、意欲的に考えたり判断したりしようとしている。
【数学への関心・意欲・態度】 - 平行線の性質や三角形の角、三角形の合同条件などの知識や技能を活用しながら、事象を論理的に考察し表現したり、その過程を振り返って考えを深めたりすることができる。
【数学的な見方や考え方】 - 平行線の性質や三角形の角の性質、三角形の合同条件を数学の用語や記号を用いて表現することができる。
【数学的な技能】 - 平行線の性質や三角形の角、三角形の合同条件を理解したり、論理的な説明の必要性を理解したりしている。
【数量や図形などについての知識・理解】
展開
- 1, 2
-
多角形の内角の和の求め方を考える。
- 3
-
多角形の外角の和の求め方を考える。
- 4
-
対頂角の意味を理解し、対頂角は等しいことを、論理的に筋道を立てて説明する。また、同位角、錯角の意味を理解する。
- 5
-
平行線と同位角の関係を基本性質として確認し、平行線と錯角の関係を、論理的に筋道を立てて説明する。
- 6
-
三角形の内角の和が180゜であることを、論理的に筋道を立てて説明する。
- 7
-
三角形の内角、外角の性質を利用して、角の大きさを求める。
多角形の内角の和、外角の和の性質を利用して、角の大きさを求める。 - 8
-
角の大きさの求め方を、補助線や根拠となる図形の性質を明らかにして説明する。
- 9
-
既習事項を活用していろいろな問題を解く。
- 10
-
合同な図形の表し方を理解する。
合同な図形の性質を見いだす。 - 11
-
実測をもとに合同な三角形を描くことを通して、三角形の合同条件を導く。
- 12
-
三角形が合同かどうかを、三角形の合同条件を使って判断することができる。
- 13
-
事柄の仮定と結論の意味を理解する。
- 14
-
根拠となる事柄を明らかにして、簡単な図形の性質を証明する。
- 15
-
補助線や合同な図形の性質を用いて、角の大きさの求め方を説明する。(本時)
- 16
- 既習事項を活用していろいろな問題を解く。
「主体的・対話的で深い学び」の視点からの授業改善
本時のねらい
補助線や合同な図形の性質を用いて、角の大きさの求め方を説明することができる。
授業場面より
-
①問題解決の見通しを持つ
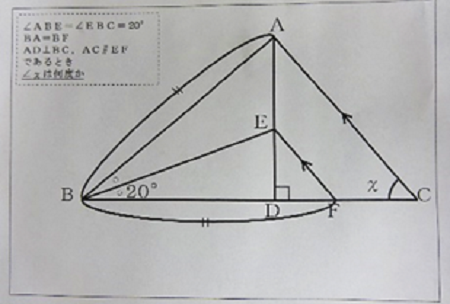
問題の見通しを持つ場面です。教師は、既習事項を活用して問題を解くことができるように、「対頂角は等しい」「2直線が平行ならば、同位角、錯角は等しい」「三角形の内角の和は180°である」などの生徒の気付きを全体で共有していきます。また、必要に応じて、問題を解決するための情報について尋ねたり、説明したりしてもよいことを確認します。それが、生徒の「∠ABE=∠EBD=20°(仮定)」「△ABDで、∠BAD=50°」「△ABEで、∠BEA=110°」「△EBDで、∠BED=70°」など分かることを明らかにしながら問題の解決に向かう主体的な姿につながりました。
-
②問いを顕在化する

明らかになったことを踏まえ、どの角の大きさが分かれば∠ACBの大きさが分かるのか話し合う場面です。教師は、生徒の「どの角の大きさに着目して考えているか」について耳を傾けていきます。その中で、∠BFEに着目している生徒に、その角に着目して考えている根拠を尋ね、個人の問いを全体の問いへと顕在化していきます。その際、グループでも、なぜその生徒が∠BFEに着目しているのかを話し合うことができるように間を大切にしていきます。このような教師の支援が、「∠BFEが分かると平行線の同位角より、∠ACBが求まる。」というさらなる解決の見通しにつながりました。
-
③互いの考えを比較・検討する

∠BFEの求め方について個人で考えたり、互いの考えを比較・検討したり行き来する場面です。教師は、個人で考える場面では、必要に応じて、直線や三角形の角の大きさを使っても解けないことを確認し、角度だけからの方向性を変え、別の既習事項の活用を促していきます。互いの考えを比較・検討する場面では、どの図形に着目して考えているのか、互いの考えの根拠を明らかにしながら共通点や相違点に目を向けて考えられるように話合いをコーディネイトしていきます。それが、△BAE≡△BFEという合同の図形に着目して、∠BFEについて考えようとする、これまでにない、合同な図形の性質を利用して角度を求めようとする視点を変えた生徒の学びにつながりました。
-
④学びのよさを自覚する

学習をまとめ、振り返る場面です。教師は、合同な三角形に着目し、対応する辺の長さや角の大きさが等しいことを利用して角の大きさを求められるよさが実感できる適用問題を用意しました。また、今後生かしていきたいことという視点を提示し、自分の学びを見つめ直すことのできる場を確保しています。それが、「みんなの意見を聞くことで、視点を変えて考える重要性に気がついた。この問題では、角度だけ考えて出ないときは、合同も考えていく必要があることが分かった。」「角度を求めるときは、合同な図形の性質も利用できるので今後、問題を解くときに使っていきたい。」という本時の学習で考えたことを今後に結び付けていこうとする姿につながりました。
報告者:研修協力員 稲岡

