アクティブ・ラーニング授業実践事例
学校名:廿日市市立四季が丘小学校
教科等:5年算数科(平成28年11月)
単元名:面積
根拠を明らかにして説明する力を伸ばしたい
 見通しを持つ
見通しを持つ 互いの考えを比較する
互いの考えを比較する 知識や技能を活用する
知識や技能を活用する
実践の背景
- 実践校は団地内の全校児童約330名の小学校です。
- 学校で育成を目指す資質・能力を、「課題発見力」、「思考力・判断力・表現力」、「主体性」、「自己肯定感」の4つに整理し、学校教育目標「夢と志をもってチャレンジするたくましい児童の育成」を目指し、学び合いを通した授業改善に取り組んでいます。
授業改善のアプローチ
- 本単元では、直線で囲まれた基本的な図形の面積を計算によって求めたり、その求め方を具体物、言葉、数、図、式を用いて考え、説明したりすることで、「根拠を明らかにして説明する力」の育成を目指しています。
- 「学校案内をするため、小学校の敷地の面積を求めたい」という単元を通して追究する学習課題を設定し、根拠を明らかにして求め方を説明する場面を設定します。
- 複数の考え方を比べることで、「直線で囲まれた図形の面積を求める際には、直角が関連する辺などの長さに着目する」という、直線で囲まれた基本的な図形の面積を求める際の視点を明らかにします。
単元づくりのポイント
目標
- 既習の正方形や長方形の面積の求め方に帰着させて考えることで、三角形、平行四辺形、ひし形、台形の面積を求めることができるというよさに気付き、進んで活用しようとしている。
【算数への関心・意欲・態度】 - 三角形、平行四辺形、ひし形、台形の面積の求め方を考えたり、公式を導き出したりすることができる。
【数学的な考え方】 - 三角形、平行四辺形、ひし形、台形の面積を公式を用いて求めることができる。
【数量や図形についての技能】 - 面積についての感覚を豊かにするとともに必要な部分の長さを用いることで、三角形、平行四辺形、ひし形、台形の面積は計算によって求めることができることを理解している。
【数量や図形についての知識・理解】
展開
面積(全13時間扱い中第10時)
- 1
- 三角形の面積を求める公式を作る。(4)
- 2
- いろいろな四角形の面積を求める公式を作る。(6)(本時)
- 3
- 面積の変化の様子を調べる。(1)
- 4
- これまでの学習をまとめ、振り返る。(2)
「主体的・対話的で深い学び」の視点からの授業改善
本時のねらい
- 三角形や長方形などの既習の面積の求め方を使って、ひし形の面積の求め方を考え、説明することができる。
授業場面より
-
①考え方の見通しを持つ
本時はひし形の面積の求め方を考えます。
児童はひし形の面積を求める際に、これまでの学びを生かし、三角形や長方形などの面積の求め方がどう使えるか考えます。
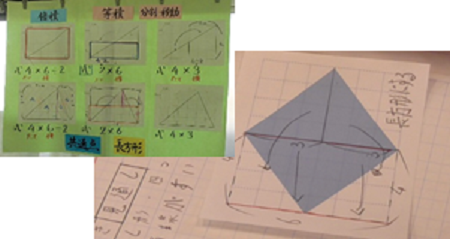
児童が考える際の拠り所となるように、教師は前時までに児童と整理した面積の求め方を教室に常時掲示しています。
本時は、3通りの考えがあるのではないかと、児童が考えました。
・【分割・移動】2本の対角線で4つの直角三角形を作り、移動する
・【倍積】ひし形を囲む長方形を使う
・【分割】1本の対角線で2つの二等辺三角形を作る -
②グループで考え方を整理する

児童は前述の3通りの考えの中から、より詳しく考えたいものを1つを選び、似た見通しを持つ児童による4人程度のグループで、考え方を整理していきます。
例えばあるグループは、「2本の対角線で4つの直角三角形を作り、その内の2つを移動することで長方形ができるからひし形の面積は、対角線×対角線÷2で求められる」と、図と式を用いてまとめました。
このとき教師は、グループで考え方を整理する目的を「相手に考え方が伝わりやすいようにしよう」と示します。
児童は、図を動かして考えるということを矢印を用いて表したり、式の中の数が何を表しているか言葉をつけたりし、考え方をホワイトボードにまとめます。 -
③全体で考え方の共通点を探る

各グループでまとめた3通りの考え方の共通点を全体で共有し、ひし形の面積の求め方を整理します。
例えば、ひし形を囲む長方形を使って、面積の求め方を考えたグループは、2つの式(①縦×横÷2、②対角線×対角線÷2)ができてどちらにすればよいか判断に迷っていることを全体に問いかけました。
ある児童が、「ひし形の面積を求めるから、長方形の縦、横より、ひし形の対角線を使った式の方がいいのではないか」という意見を述べます。
教師は、この発言や長方形や三角形などの面積を求める公式を踏まえ、個々の児童に判断を促します。児童の意見を整理することで、ひし形の公式を児童がつくっていきました。 -
④本時の学びをまとめる

本時の学びをまとめます。教師は、どのように考えたか、その結果、どんなことがわかったかというまとめの視点を示しました。
ひし形の面積の求め方について、ある児童は「ひし形の面積は、対角線が直角に交わっているから、長方形で囲む方法を使って考え、対角線×対角線÷2で求められる」と、考え方とその結果をまとめました。
このように教師は、様々な学習場面で、児童自らが考え、判断し、表現する場面を意図的に設定しています。さらに、児童も判断に迷うことは仲間の考えをもとに解決するという学び方を学んでいます。このことが、これまでの考えを活用することを繰り返すことにより、いろいろな図形の面積が求められることに気付き、根拠を明らかにして説明する力の育成にもつながっています。
報告者:研修協力員 木野村

